Определение среднего времени до отказа системы при «ударном» воздействии внешней среды

Функция распределения времени до отказа любой технической системы является предметом непараметри — ческого оценивания (см. § 1—3).

Получив на основе накопленного в эксплуатации ста­тистического. материала различные непараметрические оценки функций распределения времени до отказа сис­
темы, можно оценить и точность некоторых аналитиче­ских моделей, например, для вычисления среднего вре­мени до отказа системы. Эти аналитические модели могут быть построены на основе приближенного знания (или задания) ряда параметров, определяющих коли­чественно те изменения, которые происходят в системе до отказа я в конечном счете приводят к отказу системы.

Рассмотрим аналитическую модель определения среднего времени до отказа системы, в которой в про­цессе эксплуатации происходит под влиянием ударных воздействий внешней среды аддитивное накопление пов­реждений. Причем предполагаем, что ударные воздейст­вия внешней среды происходят в моменты времени, рас­пределенные по закону Пуассона с параметром І, а повреждения, наносимые каждым «ударом», распреде­лены экспоненциально е единичным средним.

Предполагая, что отказ системы может произойти только в один из моментов «ударов», введем функцию выживаемости ‘Системы г(х) и определим ее следующим образом. Пусть в момент предыдущего удара накоплен­ное в системе повреждение равно х, а в момент первого последующего удара система получает повреждение ве­личины у, тогда г(х+у) — вероятность отказа системы в момент первого последующего удара. Ясно, что функ­ция г(-) .— неубывающая функция от накопленных в системе повреждений.

Задача будет заключаться в том, чтобы определить среднее время до отказа системы, если в нулевой момент времени в ней отсутствовали повреждения. Обозначим через а(х) среднее время до отказа системы, если к рас­сматриваемому моменту накопления сумма повреждений равна х:

со

a(x)=X~4-j’ а.{х+у)г{х+у)е—Ыу, (5.13)

a

где —среднее время до следующего «удара»; второе сла­

гаемое — среднее время до отказа системы, если в момент преды­дущего удара сумма накопленного повреждения стала равной вели­чине х.

Преобразуем интегральное уравнение (5.13). Введем обозначение а(х)е~х=у(х). Тогда с учетом (5.13)

со

у(хуех=<к~1 + у{х+у)е&+У>г(х+у)е-Ус1у=

оо О

=Х->+/у {x+y)r{x+y)e*dy. (6.14)

О

После замены переменной x+y = z,

оо

у(х) =Х-}е-х+ j y(z)r(z)dz. и

Продифференцировав левую и правую часть (5.15), по­лучаем дифференциальное уравнение

УМ +v(*)rW = —(6.16)

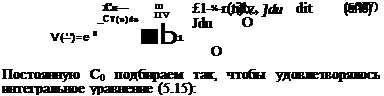Решение этого уравнения имеет вид

(5.17) и (5.18), учитывая, что а(х)е х=

сю

Л* Л V

— I [1“r(U4dU 1 _ J [I—r(u) ]du

а(х)=‘%-1є 0 J e 0 dv. (15,10)

0

Отсюда среднее время до отказа системы при отсутствии в ней повреждений

(* V

I — j [l-r(u) jdu

а(0)=^-‘ J е 0 dv. (5:20)

о

В частном случае, если функция выживаемости та­кова, что отказ наступает в тот момент, когда сумма накопленных повреждений достигает «предела прочно­сти» L,

1-, если u^L; О, если и:з=Д,

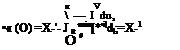получаем среднее время до отказа

L со

=Я~1 J. dv+%-1 J e-^~L4v=-t[L+> 1].

0 L

Нетрудно записать в этом частном случае и среднее вре­мя до отказа, если уровень повреждений достиг величи­ны x(x<L)

со

а(ж) =Х“1етах(°’ *-Ь) [ e-max(0,

О

оо L

=%~х J е-тах(°’ ”-г-)Дц=Х,-‘ dv-Ь (5.21)

-V Л*

Глава 6

ОРГАНИЗАЦИЯ ОБРАБОТКИ ДАННЫХ
О СОСТОЯНИИ АВИАЦИОННОЙ ТЕХНИКИ